PF-OLA provides a unified approach to express estimation models. In PF-OLA, the estimation is closely intertwined with the actual computation, with both clearly separated from query execution. Any computation is expressed as a Generalized Linear Aggregate (GLA). The user is responsible for implementing a standard interface while the framework takes care of all the issues related to parallel execution and data flow. Adding online estimation to the computation is a matter of extending the GLA state and interface with constructs corresponding to the estimator. In order to apply a different estimation model to a computation, a corresponding GLA has to be implemented. No changes have to be made to the implementation of the computation or to the implementation of the framework. This provides tremendous flexibility in designing a variety of estimation models. The complete system re-implementation is avoided in PF-OLA through the use of the generic GLA mechanism to express both computation as well as estimation. The framework defines only the execution strategy without imposing any limitation on the actual computation. As long as the user-provided computation and estimation model can be expressed using the generic mechanism, there is no need to change the PF-OLA implementation. The complexity of the tasks that can be expressed with the GLA mechanism ranges from simple and group-by aggregations to clustering and convex optimization problems applied in machine learning.

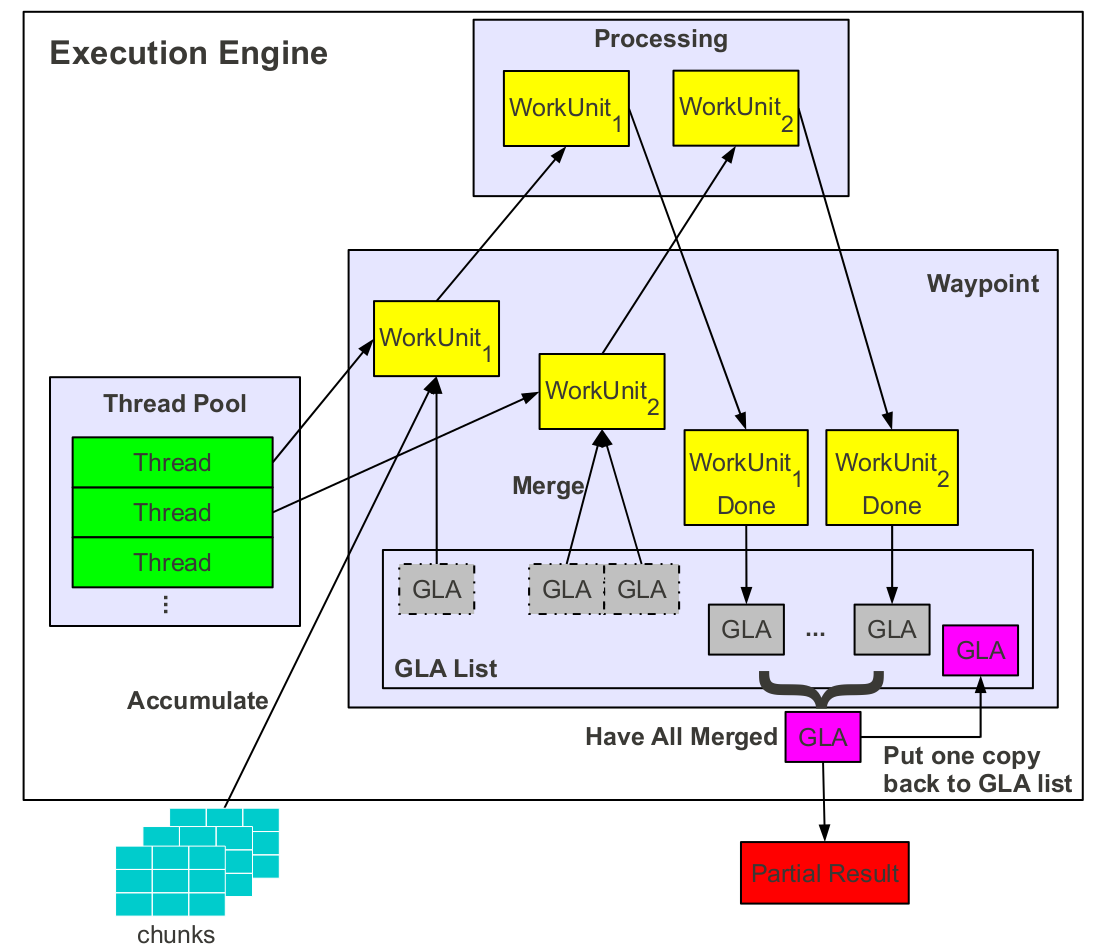
PF-OLA overlaps online estimation and actual query processing at all levels of the system and applies multiple optimizations. Abstractly, this corresponds to executing two simultaneous GLA computations. Rather than treating actual computation and estimation as two separate GLAs, we group everything into a single GLA. A partial result request triggers the merging of all existent GLAs, those inside the waypoint as well as those modified upon by a work unit. The resulting GLA is the partial result. Unlike the final result which is extracted from the waypoint and passed for further merging across the nodes, a copy of the partial result needs to be kept inside the waypoint and used for the final result computation. The newly arriving chunks are processed as before. The result is a completely new list of GLA states. The local GLA resulted through merging is added to this new list once the merging process ends.
PF-OLA processes partial result requests at any rate, at any point during query execution, and with the least amount of synchronization among the processing nodes. In the normal situation, a partial result request follows exactly the same path as a new GLA computation. Problems arise when multiple requests overlap, when requests are sent during the final result aggregation phase, and when there are nodes who have finished local processing and nodes who have not. All these scenarios are likely to appear given the asynchronous nature of the requests and of the processing. A partial result request which arrives while a particular node is still processing a previous request is discarded. The partial result generated for the earliest request is returned for all the discarded requests. A partial request received at the execution engine during the local GLA aggregation stage is discarded given that the same final GLA would be produced nonetheless. If a node has finished local processing and a partial result request is received, the node returns the local GLA for merging with the partial/final GLAs from the other nodes. This allows for online estimates to be produced even when there is considerable discrepancy in processing speed across nodes.
We design an asynchronous sampling estimator specifically targeted at parallel online aggregation. The estimator is defined over multiple data partitions which can be independently sampled in parallel. This allows for accurate estimates to be computed even when there is considerable variation between the sampling rate across partitions. We analyze the properties of the estimator and compare it with two other sampling-based estimators proposed for parallel online aggregation---a synchronous estimator and a stratified sampling estimator. All these estimators are expressed using the extended GLA interface and executed without any changes to the framework, thus proving the generality of our approach. We run an extensive set of experiments to benchmark the estimator. When executed by the framework over a massive 8TB TPC-H instance, the estimator provides accurate confidence bounds early in the execution even when the cardinality of the result is seven orders of magnitude smaller than the dataset size or when data are skewed without incurring any noteworthy overhead on top of the normal execution. Moreover, the estimator exhibits high resilience in the wake of processing node delays and failures.