
There are multiple aspects that distinguish the EXTASCID storage manager from traditional database storage managers. First, it supports natively relational data as well as multi-dimensional arrays. Second, and most important, the storage manager operates as an independent component that reads data asynchronously and pushes it for processing. It is the storage manager rather than the execution engine in control of the processing through the speed at which data are read from disk. And third, in order to support a highly-parallel execution engine consisting of multiple execution threads, the storage manager itself uses parallelism for simultaneously reading multiple data partitions.
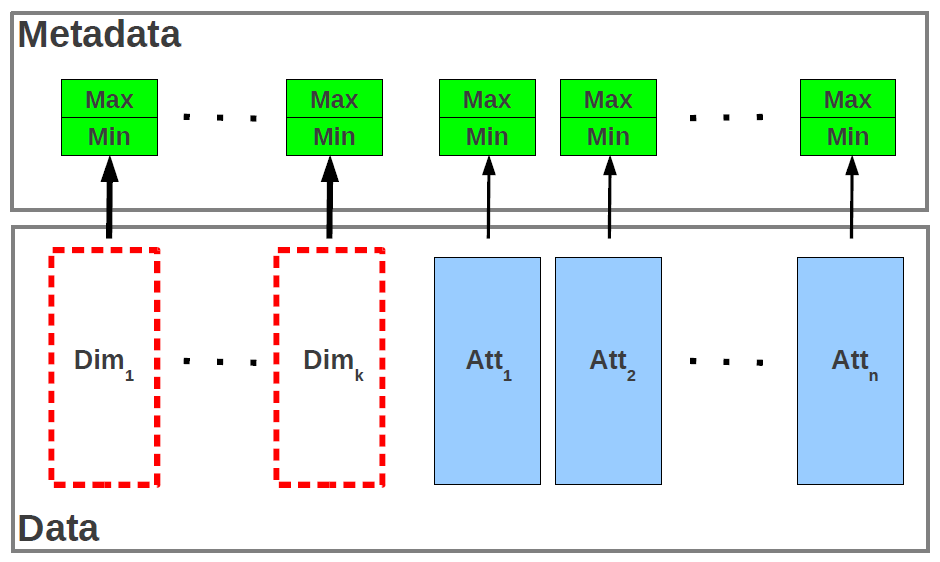
The figure depicts the generic structure of an EXTASCID chunk containing metadata to support range-based data partitioning. It is important to point out that this structure is directly applicable both to relational data as well as arrays. For unordered relations, the dimensions do not exist-there are only attributes. For arrays, dimensions form a key. They have to be represented explicitly for sparse arrays, while in the case of dense arrays the dimensions can be inferred from the position in the chunk when data are stored in a pre-determined order. The metadata contain the minimum and maximum values for each dimension and attribute and are stored in the system catalog. They represent a primitive form of indexing. Different chunking strategies generate different ranges for the (Min, Max) metadata. The ranges allow for immediate detection of the chunks that need to be processed in subsampling queries-a large class in array processing. The actual data are vertically partitioned, with each column stored in a separate set of disk blocks. This allows only for the required columns to be read for each query, thus minimizing the I/O bandwidth required for processing. While in the case of sparse arrays and relations there is not much beyond using the metadata to determine if a chunk is required for processing in a subsample or selection query, dense arrays provide further optimization opportunities. To be precise, the dimensions can be discarded altogether if the data inside the chunk are stored sorted along a known order of the dimensions. This optimization is known as dimension or index suppression and can reduce the amount of data read from disk even further. In EXTASCID the chunks required for a subsampling/selection query can be determined based on the (Min, Max) metadata, without actually reading the chunks from disk. This simple form of indexing can result in significant I/O reduction, especially for small range subsampling queries.
The EXTASCID APPLY+ operator requires grouping based on a user-defined neighborhood function followed by applying a user-defined aggregate function for all (or a subset of) cells in the array and their corresponding neighbors. The relational representation of APPLY+ consists in a structural self-join based on the neighborhood function followed by a group-by aggregation using the user-defined aggregate function. The problem with this two-operator representation is caused by the standard relational JOIN operator which does not consider the ordered array structure. The neighborhood function can be implemented either as a nested-loop join due to the complex join condition or as a series of self-joins. Both solutions are inefficient. Consequently, APPLY+ is implemented in EXTASCID as a single specialized instance of the GLA metaoperator-the APPLY+ GLA. APPLY+ GLA works as follows. In BeginChunk, array cells are sorted such that they are accessed optimally in Accumulate. Additionally, any other pre-processing required by the neighborhood or aggregate functions, e.g., reinitialize the GLA state, is invoked in BeginChunk. Array cells are grouped according to the neighborhood function in Accumulate, while the aggregate is computed in EndChunk. The simplest implementation of neighborhood grouping is to assign each cell to all the groups it is part of. The completed aggregates can be materialized in EndChunk in order to reduce memory consumption. Aggregate computation for cells that have neighbors outside of the chunk requires careful consideration. Essentially, the aggregate cannot be computed until all the cells become available in the same GLA. In EXTASCID, this is realized through the parallel merging mechanism provided by the GLA metaoperator. It is important to notice though that the amount of data transferred between GLAs is limited to what is required for the aggregate computation. This is represented exclusively by the GLA state. It is never the case that an entire chunk is passed from one worker node to another if only the border cells are used. An alternative strategy that avoids merging altogether when the neighborhood function is bounded - at the expense of increased storage and more complicated chunk management - is to enforce that aggregate computation is always confined to a chunk, thus allowing for full parallel execution across chunks. This is known as overlapping and requires cell replication across multiple chunks. APPLY+ GLA can take advantage of overlapping with minimal modifications. The Merge and Terminate methods are not required anymore since the entire computation is finalized in EndChunk. BeginChunk combines the overlapped data with the actual chunk to make them available as a whole in Accumulate.
UC Merced | EECS | Home | GLADE