pegasos.h provides a basic implementation of the PEGASOS [9] linear SVM solver.
Overview
PEGASOS solves the linear SxVM learning problem
![\[ \min_{w} \frac{\lambda}{2} \|w\|^2 + \frac{1}{m} \sum_{i=1}^n \ell(w; (x_i,y_i)) \]](form_255.png)
where  are data vectors in
are data vectors in 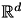 ,
, 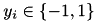 are binary labels,
are binary labels, 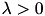 is the regularization parameter, and
is the regularization parameter, and
![\[ \ell(w;(x_i,y_i)) = \max\{0, 1 - y_i \langle w,x_i\rangle\}. \]](form_258.png)
is the hinge loss. The result of the optimization is a model  that yields the decision function
that yields the decision function
![\[ F(x) = \operatorname{sign} \langle w, x\rangle. \]](form_260.png)
It is well known that the hinge loss is a convex upper bound of the i01-loss of the decision function:
![\[ \ell(w;(x,y)) \geq \frac{1}{2}(1 - y F(x)). \]](form_261.png)
PEGASOS is accessed by calling vl_pegasos_train_binary_svm_d or vl_pegasos_train_binary_svm_f, operating respectively on double or float data.
Algorithm
PEGASOS [9] is a stochastic subgradient optimizer. At the t-th iteration the algorithm:
- Samples uniformly at random as subset
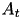 of k of training pairs
of k of training pairs 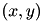 from the m pairs provided for training (this subset is called mini batch).
from the m pairs provided for training (this subset is called mini batch). - Computes a subgradient
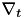 of the function
of the function 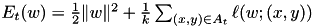 (this is the SVM objective function restricted to the minibatch).
(this is the SVM objective function restricted to the minibatch). - Compute an intermediate weight vector
 by doing a step
by doing a step 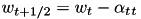 with learning rate
with learning rate 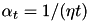 along the subgradient. Note that the learning rate is inversely proportional to the iteration numeber.
along the subgradient. Note that the learning rate is inversely proportional to the iteration numeber. - Back projects the weight vector
 on the hypersphere of radius
on the hypersphere of radius 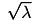 to obtain the next model estimate
to obtain the next model estimate 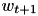 :
:
The hypersfere is guaranteed to contain the optimal weight vector![\[ w_t = \min\{1, \sqrt{\lambda}/\|w\|\} w_{t+1/2}. \]](form_271.png)
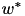 [9] .
[9] .
VLFeat implementation fixes to one the size of the mini batches 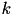 .
.
Bias
PEGASOS SVM formulation does not incorporate a bias. To learn an SVM with bias, the each data vector  can be extended by a constant component
can be extended by a constant component 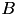 (called
(called biasMultiplier in the code). In this case, the model 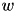 has dimension
has dimension 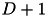 and the SVM discriminat function is given by
and the SVM discriminat function is given by 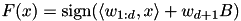 . If the bias multiplier B is large enough, the weight
. If the bias multiplier B is large enough, the weight 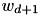 remains small and it has small contribution in the SVM regularization term
remains small and it has small contribution in the SVM regularization term 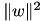 , better approximating the case of an SVM with bias. Unfortunately, setting the bias multiplier
, better approximating the case of an SVM with bias. Unfortunately, setting the bias multiplier 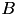 to a large value makes the optimization harder.
to a large value makes the optimization harder.
Restarting
VLFeat PEGASOS implementation can be restatred after any given number of iterations. This is useful to compute intermediate statistics or to load new data from disk for large datasets. The state of the algorithm, which is required for restarting, is limited to the current estimate 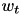 of the SVM weight vector and the iteration number
of the SVM weight vector and the iteration number 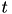 .
.
Permutation
VLFeat PEGASOS can use a user-defined permutation to decide the order in which data points are visited (instead of using random sampling). By specifying a permutation the algorithm is guaranteed to visit each data point exactly once in each loop. The permutation needs not to be bijective. This can be used to visit certain data samples more or less often than others, implicitly reweighting their relative importance in the SVM objective function. This can be used to blanace the data.
Non-linear kernels
PEGASOS can be extended to non-linear kernels, but the algorithm is not particularly efficient in this setting [1]. When possible, it may be preferable to work with explicit feature maps.
Let 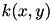 be a positive definite kernel. A feature map is a function
be a positive definite kernel. A feature map is a function  such that
such that  . Using this representation the non-linear SVM learning objective function writes:
. Using this representation the non-linear SVM learning objective function writes:
![\[ \min_{w} \frac{\lambda}{2} \|w\|^2 + \frac{1}{m} \sum_{i=1}^n \ell(w; (\Psi(x)_i,y_i)). \]](form_282.png)
Thus the only difference with the linear case is that the feature  is used in place of the data
is used in place of the data  .
.
 can be learned off-line, for instance by using the incomplete Cholesky decomposition
can be learned off-line, for instance by using the incomplete Cholesky decomposition 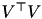 of the Gram matrix
of the Gram matrix ![$ K = [k(x_i,x_j)] $](form_284.png) (in this case
(in this case 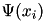 is the i-th columns of V). Alternatively, for additive kernels (e.g. intersection, Chi2) the explicit feature map computed by homkermap.h can be used.
is the i-th columns of V). Alternatively, for additive kernels (e.g. intersection, Chi2) the explicit feature map computed by homkermap.h can be used.