VLFeat - Documentation

Author:: Andrea Vedaldi

homkermap.h implements the homogeneous kernel maps introduced in [13] , [14] . Such maps are efficient linear representations of popular kernels such as the intersection, 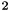$\chij^2$ , and Jensen-Shannon ones.

Overview

The homogeneous kernel map is a finite dimensional linear approximation of homgeneous kernels, including the intersection, 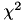$\chi^2$ , and Jensen-Shannon kernels. These kernels are ffrequently used in computer vision applications because they are particular suitable for data in the format of histograms, which encompasses many visual descriptors used.

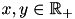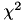Let $x,y \in \mathbb{R}_+$ be non-negative scalars and let $k(x,y) \in \mathbb{R}$ be an homogeneous kernel such as the $\chi^2$ and or the intersection ones:

$k_{\mathrm{inters}}(x,y) = \min\{x, y\}, \quad k_{\chi^2}(x,y) = 2 \frac{(x - y)^2}{x+y}.$

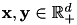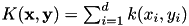For vectorial data $\mathbf{x},\mathbf{y} \in \mathbb{R}_+^d$ , the homogeneous kernels in an additive combination $K(\mathbf{x},\mathbf{y}) = \sum_{i=1}^d k(x_i,y_i)$ .

The homogeneous kernel map of order 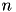$ n $ is a vectorial function 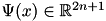$\Psi(x) \in \mathbb{R}^{2n+1}$ such that, for any choice of 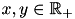$x, y \in \mathbb{R}_+$ , one has

$k(x,y) \approx \langle \Psi(x), \Psi(y) \rangle.$

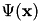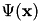Given the feature map for the scalar case, the corresponding feature map $\Psi(\mathbf{x})$ for the vectorial case is obtained by stacking $[\Psi(x_1), \dots, \Psi(x_n)]$ . Note that the combined feature $\Psi(\mathbf{x})$ has dimension $ d(2n+1) $ .

Using linear analysis tools (e.g. a linear support vector machine) on top of dataset that has been encoded by the homogeneous kernel map is therefore approximately equivalent to using a method based on the corresponding non-linear kernel.

Extension to the negative reals

Any positive (semi-)definite kernel 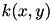$ k(x,y) $ defined on the non-negative reals 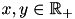$x,y \in \mathbb{R}_+$ can be extended to the entiere real line by using the definition:

$k_\pm(x,y) = \operatorname{sign}(x) \operatorname{sign}(y) k(|x|,|y|).$

The homogeneous kernel map implements this extension by defining 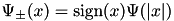$\Psi_\pm(x) = \operatorname{sign}(x) \Psi(|x|)$ . Note that other extensions are possible, such as

$k_\pm(x,y) = H(xy) \operatorname{sign}(y) k(|x|,|y|)$

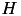where $ H $ is the Heavyside function, but may require higher dimensional feature maps.

Homogeneity order

Any (1-)homogeneous kernel 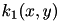$ k_1(x,y) $ can be extended to a so called gamma-homgeneous kernel 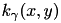$k_\gamma(x,y)$ by the definition

$k_\gamma(x,y) = (xy)^{\frac{\gamma}{2}} \frac{k_1(x,y)}{\sqrt{xy}}$

Smaller value of 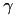$\gamma$ enhance the kernel non-linearity and are sometimes beneficial in applications (see [1,2] for details).

Windowing and period

This section discusses aspects of the homogeneous kernel map which are more technical and may be skipped. The homogeneous kernel map approximation is based on periodicizing the kernel; given the kernel signature

$\Kappa(\lambda) = k(e^{\frac{\lambda}{2}}, e^{-\frac{\lambda}{2}})$

the homogeneous kerne map is a feature map for the windowed and periodicized kernel whose signature is given by

$\hat{\mathcal{K}}(\lambda) = \sum_{i=-\infty}^{+\infty} \mathcal{K}(\lambda + k \Lambda) W(\lambda + k \Lambda)$

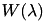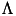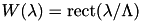where $W(\lambda)$ is a windowing function and $\Lambda$ is the period. This implementation of the homogeneous kernel map supports the use of a uniform window ( $W(\lambda) = 1$ ) or of a rectangular window ( $W(\lambda) = \operatorname{rect}(\lambda/\Lambda)$ ). Note that 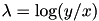$\lambda = \log(y/x)$ is equal to the logarithmic ratio of the arguments of the kernel. Empirically, the rectangular window seems to have a slight edge in applications.

Usage

The homogeneous kernel map is implemented as an object of type VlHomogeneousKernelMap. To use thois object, first create an instance by vl_homogeneouskernelmap_new, then use vl_homogeneouskernelmap_evaluate_d or vl_homogeneouskernelmap_evaluate_f (depdening on whether the data is double or float) to compute the feature map $\Psi(x)$ . When done, dispose of the object by calling vl_homogeneouskernelmap_delete.

The constructor vl_homogeneouskernelmap_new requires the kernel type kernel (see VlHomogeneousKernelType), the homogeneity order gamma (use one for the standard kernels), the approximation order order (usually order one is enough), the period period (use a negative value to use the default period), and a window type window (use VlHomogeneousKernelMapWindowRectangular if unsure). The approximation order trades off the quality and dimensionality of the approximation. The resulting feature map $\Psi(x)$ , computed by vl_homogeneouskernelmap_evaluate_d or vl_homogeneouskernelmap_evaluate_f , is 2*order+1 dimensional.

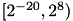The code pre-computes the map $\Psi(x)$ for efficient evaluation. The table spans values of $ x $ in the range $[2^{-20}, 2^{8})$ . In particular, values smaller than $2^{-20}$ are treated as zeroes (which result in a null feature).

Technical details

The code uses the expressions given in [13] , [14] to compute in closed form the maps $\Psi(x)$ for the suppoerted kernel types. For efficiency reasons, it tabulates $\Psi(x)$ when the homogeneous kernel map object is created.

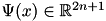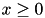The interal table stores $\Psi(x) \in \mathbb{R}^{2n+1}$ for $x \geq 0$ by sampling this variable. In particular, x is decomposed as

  x = mantissa * (2**exponent),
  minExponent <= exponent <= maxExponent,
  1 <= matnissa < 2.

Each octave is further subdivided in numSubdivisions sublevels.