Old CodeSupporting code for our manuscript, "Spectral solution of delayed random walks:" ssdrw.tar.gzThis .tar.gz file contains all Matlab codes necessary for reproducing the Fig. 1-2 and Fig. 4 in the manuscript, together with code that can be used to implement the spectral method on other problems. After downloading, gunzipping, and untarring the file, please read the README file for details. Finite-volume solver for 2D Maxwell's equations: fvtri.tar.gz This is a Matlab code that solves the planar Maxwell system detailed in "Kirchhoff's laws as a finite volume method for a planar Maxwell system," IEEE Trans. Ant. Prop., 59(10), [pdf] [link]. In the paper, we use a rectangular mesh; the code available here works with an unstructured triangular mesh. To run the code, you will need to use Persson and Strang's DistMesh, available [here]. Once you have downloaded distmesh and added it to your Matlab path, you should be able to run the demo code "main.m" contained in the .tar.gz file linked above. The code is initially set up to run with a very coarse mesh, so that it finishes quickly. To make the mesh finer, change line 7 of the file from "fv = fvtri(0.1)" to "fv = fvtri(0.01)", and you should obtain the following three images: |
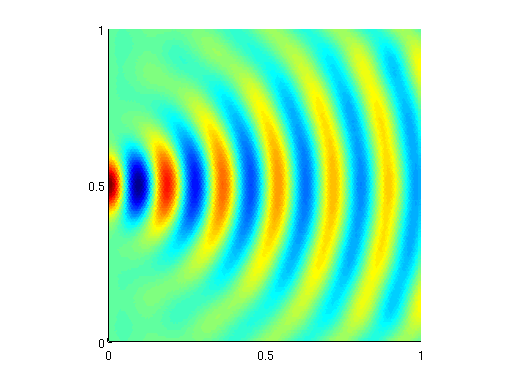 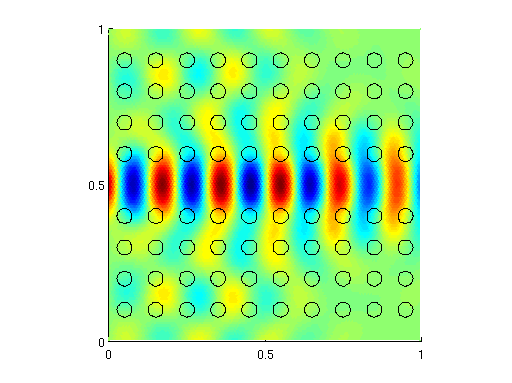 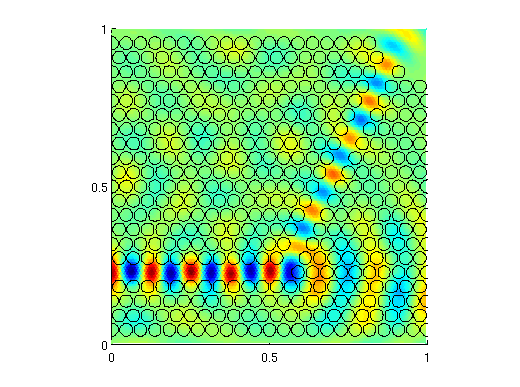 |
|
In the .tar.gz file linked above, we have bundled five .m files that
are derived from Peyre's Toolbox Graph, available
[here].
This code is available with a GPL license. Four of the five .m files are
included with no modifications. The fifth file, "compute_dual_graph.m" has
two modifications compared with the original: (1) on line 28, "nargin" has
been replaced by "nargout", and (2) on line 37, A is declared to be sparse.
|
|
Discrete Rayleigh-Sommerfeld diffraction patterns: discreteRS.nb
This is a Mathematica code that uses the lattice Green's function for the discrete Helmholtz equation to evaluate a discrete version of the Rayleigh-Sommerfeld formula. For more details, see "Diffraction on the two-dimensional square lattice," SIAM J. Appl. Math., 70(5), pp. 1389-1406. [link] |
|
All codes presented here are based upon work supported by the National Science Foundation under Grants 0913048, 0753983 and/or 0713732. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation (NSF). |
| [Home] |