We propose an in-database solution for Big Model analytics. The main idea is to offload the model to secondary storage and leverage database techniques for efficient training. The model is represented as a table rather than as an array attribute. This distinction in model representation changes fundamentally how in-database analytics tasks are carried out. We identify dot-product as the most critical operation affected by the change in model representation. Our central contribution is the first dot-product join physical database operator optimized to execute secondary storage array-relation dot-products effectively. We design the first array-relation dot-product join database operator targeted at secondary storage. We present several alternatives for implementing dot-product in a relational database and discuss their relative advantages and drawbacks. Dot-product join is a constrained instance of the SpMV kernel which is widely-studied across many computing areas, including HPC, architecture, and compilers. The paramount challenge we have to address is how to optimally schedule access to the dense relation - buffer management - based on the non-contiguous feature entries in the sparse arrays. The goal is to minimize the overall number of secondary storage accesses across all the sparse arrays. We prove that this problem is NP-hard and propose a practical solution characterized by two technical contributions. The first contribution is to handle the sparse arrays in batches with variable size determined dynamically at runtime. The second contribution is a reordering strategy for the arrays such that accesses to co-located entries in the dense relation can be shared. We devise three batch reordering heuristics - LSH, Radix, and K-center - inspired from optimizations to the SpMV kernel and evaluate them thoroughly. We show how the dot-product join operator is integrated in the gradient descent optimization pipeline for training generalized linear models.

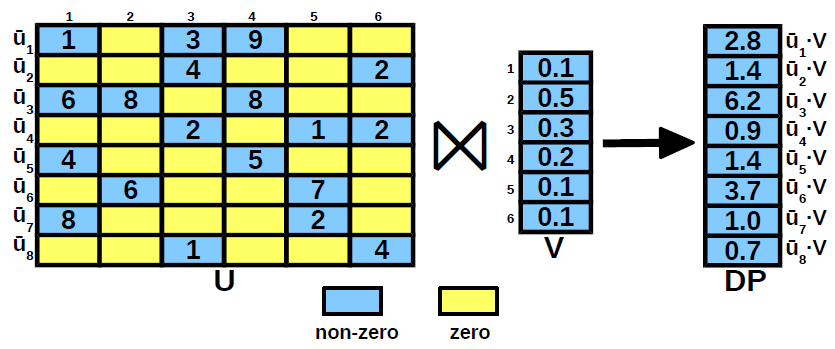
We focus on Big Model dot-product. Several aspects make this particular form of dot-product an interesting and challenging problem at the same time. First, the vector corresponding to the model V cannot fit in the available memory. Second, the vector corresponding to a training example U is sparse and the number of non-zero entries is a very small fraction from the dimensionality of the model. In these conditions, dot-product becomes highly inefficient because it has to iterate over the complete model even though only a small number of entries contribute to the result. The third challenge is imposed by the requirement to support Big Model dot-product inside a relational database where there is no notion of order - the relational model is unordered. The only solution to implement dot-product inside a database is through the UDF-UDA extensions which process a single tuple at a time. The operands U and V are declared as table attributes having ARRAY type, while the dot-product is implemented as a UDF. For reference, the existing in-database analytics alternatives treat the model as an in-memory UDA state variable. This is impossible in Big Model analytics. The research problem we study is how to design a database operator for Big Model dot-product. This operator computes the set of dot-products between the examples and the model optimally. Since the model V cannot fit in-memory, optimality is measured by the total number of secondary storage accesses. This is a good indicator for the execution time, given the simple computation required in dot-product. In addition to the main objective, we include a functional constraint in the design - results have to be generated in a non-blocking fashion. As soon as the dot-product corresponding to a training example is computed, it is made available to the calling operator/application. This requirement is essential to support SGD - the gradient descent solution used the most in practice. If we ignore the non-blocking functional constraint, the result vector is the product of sparse matrix U and vector V. This is the standard SpMV kernel which is notorious for sustaining low fractions of peak performance and for which there is a plethora of algorithms proposed in the literature. However, none of these algorithms considers the case when vector V does not fit in memory. They focus instead on the higher levels of the storage hierarchy, i.e., memory-cache and global memory - texture memory in GPU, respectively. While some of the solutions can be extended to disk-based SpMV, they are applicable only to BGD optimization which is less often used in practice. In SGD, V is updated after computing the dot-product with every vector, i.e., row of matrix U. This renders all the SpMV algorithms inapplicable to Big Model dot-product. We propose novel algorithms for this constrained version of SpMV. Since this is a special instance of SpMV, the proposed solution is applicable to the general SpMV problem.
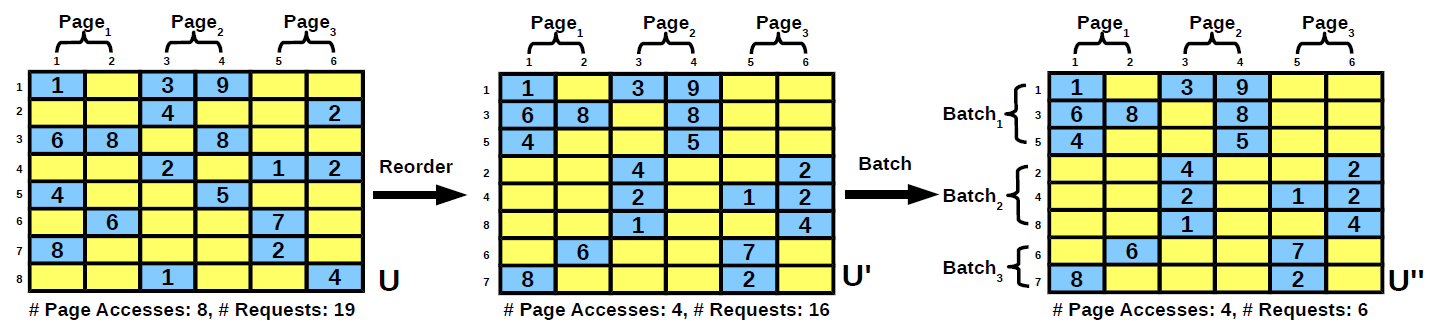
The Dot-Product Join operator pushes the aggregation inside the ARRAY-relation join and applies a series of optimizations that address the challenges to minimize the number of secondary storage accesses and the number of requests to entries in V. Given U, V, and memory budget M, Dot-Product Join Operator iterates over the pages of U and executes a three-stage procedure at page-level. The three stages are: optimization, batch execution, and dot-product computation. Optimization minimizes the number of secondary storage accesses. Batch execution reduces the number of requests to V entries. Dot-product computation is a direct call to Dot-Product that computes an entry of the DP result. Notice that generating intermediate join results and grouping are not required anymore since the entries in V corresponding to a vector are produced in a contiguous batch. We propose three heuristic algorithms that find good reorderings efficiently. The first algorithm is an LSH-based extension to nearest neighbor - the well-known approximation to minimum Hamiltonian path. The second algorithm is partition-level radix sort. The third algorithm is standard k-center clustering applied at partition-level. Vector reordering is based on permuting a set of rows and columns of a sparse matrix in order to improve the performance of the SpMV kernel. Permuting is a common optimization technique used in sparse linear algebra. The most common implementation is the reverse Cuthill-McKee algorithm (RCM) which is widely used for minimizing the maximum distance between the non-zeros and the diagonal of the matrix. Since the RCM algorithm permutes both rows and columns, it incurs an unacceptable computational cost. To cope with this, vector reordering limits permuting only to the rows of the matrix. The second task of the optimization stage is to reduce the number of page requests to the buffer manager. Even when the requested page is in the buffer, there is a non-negligible overhead in retrieving and passing the page to the dot-product join operator. A straightforward optimization is to group together requests made to indexes co-located in the same page. We take advantage of the reordering to group consecutive vectors into batches and make requests at batch-level. This strategy is beneficial because similar vectors are grouped together by the reordering. Formally, we have to identify the batches that minimize the number of page requests to V given a fixed ordering of the vectors in U and a memory budget M. Without the ordering constraint, this is the standard bin packing problem, known to be NP-hard. Due to ordering, a simple greedy heuristic that iterates over the vectors and adds them to the current batch until the capacity constraint is not satisfied is guaranteed to achieve the optimal solution. The output is a set of batches with a variable number of vectors. Given the batches extracted in the optimization stage, we compute the dot-products by making a single request to the buffer manager for all the pages accessed in the batch. It is guaranteed that these pages fit in memory at the same time. Notice, though, that vectors U are still processed one-by-one, thus, dot-product results are generated individually. While batch execution reduces the number of requests to the buffer manager, the requests consist of a set of pages. It is important to emphasize that decomposing the set request into a series of independent single-page requests is sub-optimal. In order to support set requests, the functionality of the buffer manager has to be enhanced. Instead of directly applying the replacement policy, e.g., LRU, there are two stages in handling a page set request. First, the pages requested that are memory-resident have to be pinned down such that the replacement policy does not consider them. Second, the remaining requested pages and the non-pinned buffered pages are passed to the standard replacement policy.
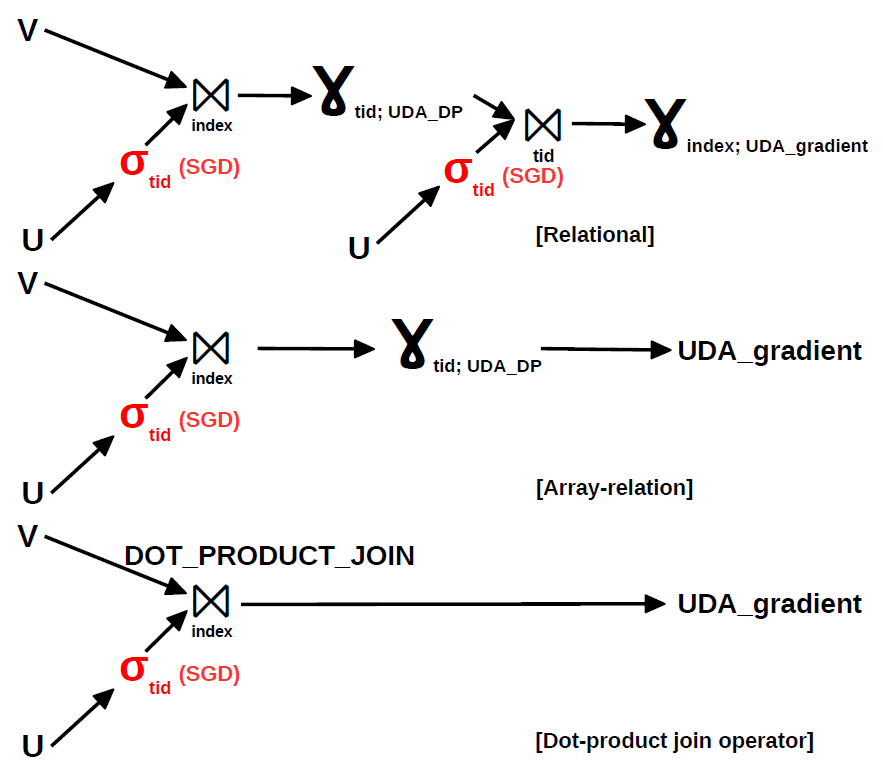
As we move from the relational solution to the proposed dot-product join operator, the query plan becomes considerably simpler. The relational solution consists of two parts. In the first part, the dot-product corresponding to a vector U is computed. Since vector components are represented as independent tuples with a common identifier, this requires a group-by on tid. However, this results in the loss of the vector components, required for gradient computation. Thus, a second join group-by is necessary in order to compute each component of the gradient. The ARRAY-relation solution is able to discard the second join group-by because it groups vector components as an array attribute of a tuple. The proposed dot-product join operator goes one step further and pushes the group-by aggregation inside the join. While this idea has been introduced in for BGD over normalized example data, the dot-product join operator considers joins between examples and the model and works for BGD and SGD alike - SGD requires only an additional selection. The main benefit of pushing the group-by aggregation inside the join is that the temporary join result is not materialized. The savings in storage can be several orders of magnitude. By discarding the blocking group-by on tid, the overall gradient computation becomes non-blocking since dot-product join is non-blocking. In order to achieve faster convergence, SGD requires random example traversals. Since dot-product join reorders the examples in order to cluster similar examples together, we expect this to have a negative effect on convergence. However, the reordering in dot-product join is only local at page-level. Thus, a simple strategy to eliminate the effect of reordering completely is to estimate the gradient at page-level. The number of steps in an iteration is equal to the number of pages. Any intermediate scheme that trades-off convergence speed with secondary storage accesses can be imagined. To maximize convergence, the data traversal orders across iterations have to be also random.