OLA in Distributed Gradient Descent Optimization
We consider the problem of distributed model calibration with iterative optimization methods, e.g., gradient descent. We argue that the incapacity to evaluate multiple parameter configurations simultaneously and the lack of support to quickly identify sub-optimal configurations are the principal causes that make model calibration difficult. It is important to emphasize that these problems are not specific to a particular model, but rather they are inherent to the optimization method used in training. The target of our methods is to find optimal configurations for the tunable hyper-parameters of the optimization method, e.g., step size, which, in turn, facilitate the discovery of optimal values for the model parameters.
We apply parallel online aggregation to identify sub-optimal configurations early in the processing by incrementally sampling the training dataset and estimating the objective function corresponding to each configuration. We design concurrent online aggregation estimators and define halting conditions to accurately and timely stop the execution. We provide efficient parallel solutions for the evaluation of the concurrent estimators and of their confidence bounds that guarantee fast convergence. The end-result is online approximate gradient descent---a novel optimization method for scalable model calibration. Our major contribution is the conceptual integration of parallel multi-query processing and online aggregation for efficient and effective large-scale model calibration with gradient descent methods.
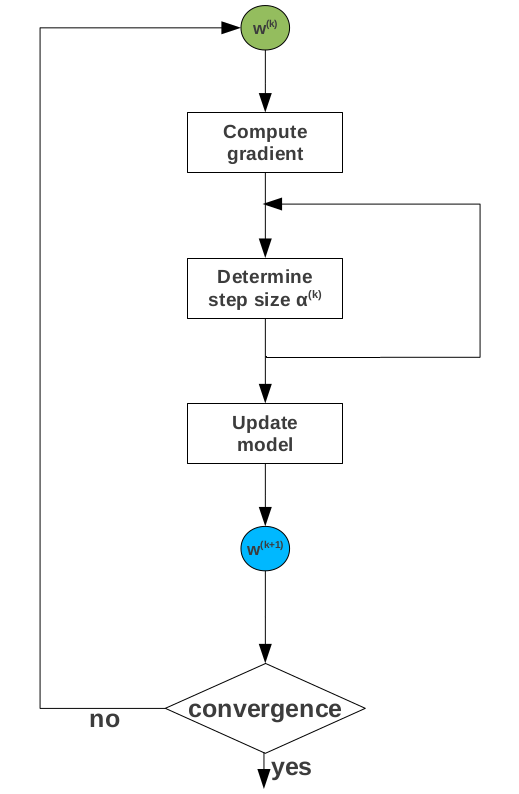
Parallel Gradient Descent
Gradient descent represents the most popular method to solve the class of optimization problems arising in machine learning training. Gradient descent is an iterative optimization algorithm that starts from an arbitrary model and computes new models such that the loss decreases at every step. The new models are determined by moving along the opposite gradient direction. The length of the move at a given iteration is known as the step size. Gradient descent is highly sensitive to the choice of the step size hyper-parameter which requires careful tuning for every dataset. The standard approach to compute the updated model once the direction of the gradient is determined is to use line search methods which require objective and gradient loss evaluation. These involve multiple passes over the entire data. The straightforward strategy to parallelize gradient descent is to overlap gradient computation across the processing nodes storing the data partitions. The partial gradients are subsequently aggregated at a coordinator node holding the current model, where a single global update step is performed in order to generate the new model. The update step requires completion of partial gradient computation across all the nodes, i.e., update model is a synchronization barrier. Once the new model is computed, it is disseminated to the processing nodes for a new iteration over the data. Parallel gradient descent works because the loss function is linearly separable. It provides linear processing speedup and logarithmic communication in the number of nodes.
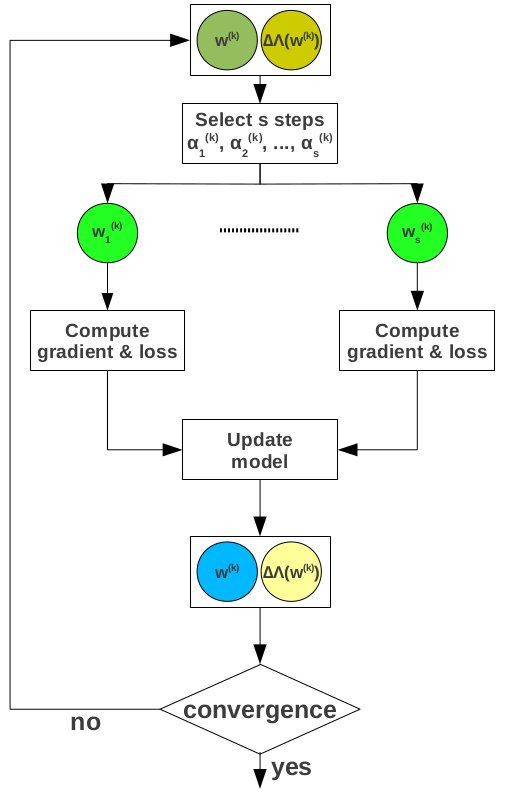
Speculative Gradient Descent
Speculative gradient descent addresses two fundamental problems---hyper-parameter tuning and convergence detection. Finding the optimal value for the hyper-parameters typically requires many trials. While convergence detection requires loss evaluation at every iteration, the standard practice is to discard detection altogether and execute the algorithm for a fixed number of iterations. Discarding loss computation increases both the number of trials in hyper-parameter tuning as well as the duration of each trial.
The main idea in speculative gradient descent is to overlap gradient and loss computation for multiple hyper-parameter configurations across every data traversal. The number of hyper-parameter configurations used at each iteration is determined adaptively and dynamically at runtime. Their values are drawn from parametric distributions that are continuously updated using a Bayesian statistics approach. Only the model with the minimum loss survives each iteration, while the others are discarded. Speculative gradient descent allows for early bad configuration identification since many trials are executed simultaneously and timely convergence detection. Overall, faster model calibration.
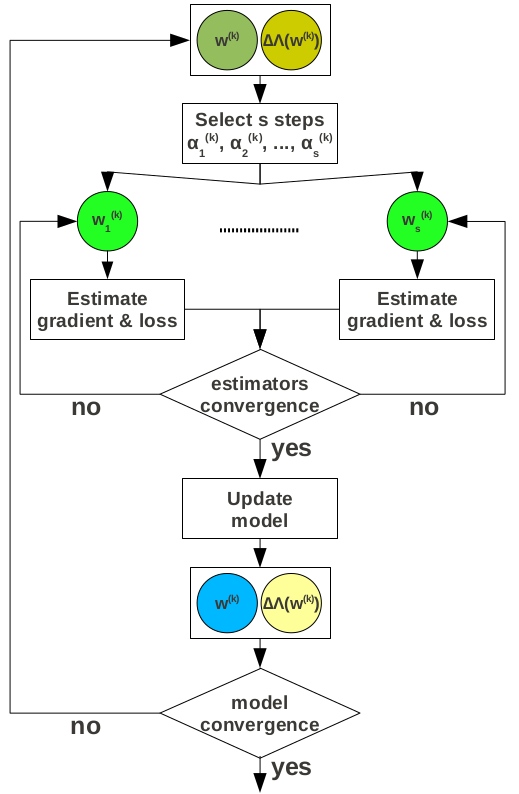
Online Approximate Gradient Descent
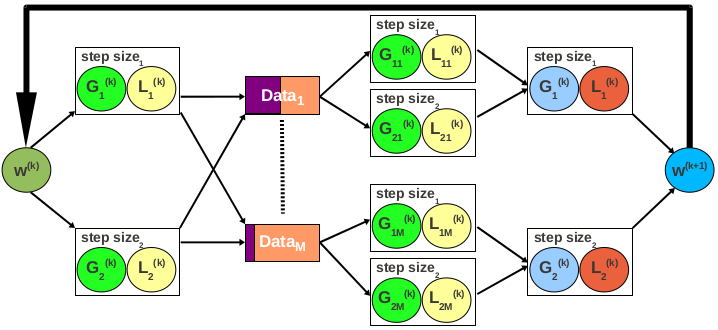
Speculative gradient descent allows for a more effective exploration of the parameter space. However, it still requires complete passes over the entire data at each iteration. Online approximate gradient descent applies online aggregation sampling to avoid this whenever possible and identify the sub-optimal hyper-parameter configurations earlier. This works because both the gradient and the loss can be expressed as aggregates in the case of linearly separable objective functions. The most important challenge we have to address is how to design halting mechanisms that allow for the speculative query execution to be stopped as early as a user-defined accuracy threshold is achieved.
In the case of gradient computation, there are $d$ aggregates---one for every dimension in the feature vector. With online aggregation active, there is an estimator and corresponding confidence bounds for every aggregate. Given a desired level of accuracy, we have to determine when to stop the computation and move to a new iteration. We measure the accuracy of an estimator by the relative error, defined as the ratio between the confidence bounds width and the estimate. What makes our problem difficult is that we have $d$ independent relative errors, one for each estimator. The simple solution is to wait until all the errors drop below the accuracy threshold. This might require processing the entire dataset even when only a few estimators do not satisfy the accuracy requirement, thus defeating the purpose of online aggregation. An alternative that eliminates this problem is to require that only a percentage of the estimators, e.g., 90%, achieve the desired accuracy. Another alternative is to define a single convergence threshold across the $d$ estimators.
While the estimators in gradient computation are independent -- in the sense that there is no interaction between their confidence bounds with respect to the stopping criterion -- the loss estimators corresponding to different step sizes are dependent. Our goal is to choose only the estimator generating the minimum loss. Whenever we determine this estimator with high accuracy, we can stop the execution and start a new iteration. Notice that finding the actual loss -- or an accurate approximation of it -- is not required if gradient descent is executed for a fixed number of iterations. We design the following algorithm for stopping loss computation. The idea is to prune as many estimators as possible early in the execution. It is important to emphasize that pruning impacts only the convergence rate---not the correctness of the proposed method. Pruning conditions are exact and approximate. All the estimators for which there exists an estimator with confidence bounds completely below their confidence bounds, can be pruned. The remaining estimators overlap. In this situation, we resort to approximate pruning. We consider three cases. First, if the overlap between the upper bound of one estimator and the lower bound of another is below a user-specified threshold, the upper estimator can be discarded with high accuracy. Second, if an estimator is contained inside another at the upper-end, the contained estimator can be discarded. The third case is symmetric, with the inner estimator contained at the lower-end. The encompassing estimator can be discarded in this case. Execution can be stopped when a single estimator survives the pruning process. If the process is executed until the estimators achieve the desired accuracy, we choose the estimator with the lowest expected value.
This project is partially supported by a Hellman Fellowship, a gift from LogixBlox, and a DOE Early Career Award. The results are published in the following papers:
-
Speculative Approximations for Terascale Analytics
by C. Qin and F. Rusu.
-
Speculative Approximations for Terascale Distributed Gradient Descent Optimization
by C. Qin and F. Rusu.
-
Scalable Analytics Model Calibration with Online Aggregation
by F. Rusu, C. Qin, and M. Torres.
UC Merced |
EECS |
Home |
OLA
Last updated: Monday, November 27, 2017