aib.h implemens the Agglomerative Information Bottleneck (AIB) algorithm as first described in [11] .
AIB takes a discrete valued feature 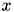 and a label
and a label 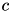 and gradually compresses
and gradually compresses 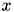 by iteratively merging values which minimize the loss in mutual information
by iteratively merging values which minimize the loss in mutual information 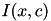 .
.
While the algorithm is equivalent to the one described in [11] , it has some speedups that enable handling much larger datasets. Let N be the number of feature values and C the number of labels. The algorithm of [11] is 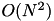 in space and
in space and 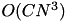 in time. This algorithm is
in time. This algorithm is 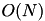 space and
space and 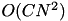 time in common cases (
time in common cases ( 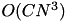 in the worst case).
in the worst case).
Overview
Given a discrete feature 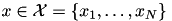 and a category label
and a category label 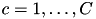 with joint probability
with joint probability 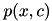 , AIB computes a compressed feature
, AIB computes a compressed feature ![$[x]_{ij}$](form_10.png) by merging two values
by merging two values 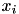 and
and 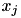 . Among all the pairs
. Among all the pairs 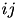 , AIB chooses the one that yields the smallest loss in the mutual information
, AIB chooses the one that yields the smallest loss in the mutual information
![\[ D_{ij} = I(x,c) - I([x]_{ij},c) = \sum_c p(x_i) \log \frac{p(x_i,c)}{p(x_i)p(c)} + \sum_c p(x_i) \log \frac{p(x_i,c)}{p(x_i)p(c)} - \sum_c (p(x_i)+p(x_j)) \log \frac {p(x_i,c)+p(x_i,c)}{(p(x_i)+p(x_j))p(c)} \]](form_14.png)
AIB iterates this procedure until the desired level of compression is achieved.
Algorithm details
Computing 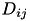 requires
requires 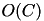 operations. For example, in standard AIB we need to calculate
operations. For example, in standard AIB we need to calculate
![\[ D_{ij} = I(x,c) - I([x]_{ij},c) = \sum_c p(x_i) \log \frac{p(x_i,c)}{p(x_i)p(c)} + \sum_c p(x_i) \log \frac{p(x_i,c)}{p(x_i)p(c)} - \sum_c (p(x_i)+p(x_j)) \log \frac {p(x_i,c)+p(x_i,c)}{(p(x_i)+p(x_j))p(c)} \]](form_14.png)
Thus in a basic implementation of AIB, finding the optimal pair 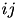 of feature values requires
of feature values requires 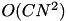 operations in total. In order to join all the
operations in total. In order to join all the 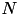 values, we repeat this procedure
values, we repeat this procedure 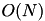 times, yielding
times, yielding 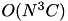 time and
time and 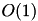 space complexity (this does not account for the space need to store the input).
space complexity (this does not account for the space need to store the input).
The complexity can be improved by reusing computations. For instance, we can store the matrix ![$D = [ D_{ij} ]$](form_21.png) (which requires
(which requires 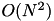 space). Then, after joining
space). Then, after joining 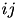 , all of the matrix D except the rows and columns (the matrix is symmetric) of indexes i and j is unchanged. These two rows and columns are deleted and a new row and column, whose computation requires
, all of the matrix D except the rows and columns (the matrix is symmetric) of indexes i and j is unchanged. These two rows and columns are deleted and a new row and column, whose computation requires 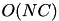 operations, are added for the merged value
operations, are added for the merged value 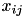 . Finding the minimal element of the matrix still requires
. Finding the minimal element of the matrix still requires 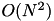 operations, so the complexity of this algorithm is
operations, so the complexity of this algorithm is 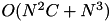 time and
time and 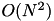 space.
space.
We can obtain a much better expected complexity as follows. First, instead of storing the whole matrix D, we store the smallest element (index and value) of each row as 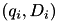 (notice that this is also the best element of each column since D is symmetric). This requires
(notice that this is also the best element of each column since D is symmetric). This requires 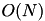 space and finding the minimal element of the matrix requires
space and finding the minimal element of the matrix requires 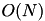 operations. After joining
operations. After joining 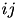 , we have to efficiently update this representation. This is done as follows:
, we have to efficiently update this representation. This is done as follows:
- The entries
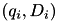 and
and 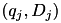 are deleted.
are deleted. - A new entry
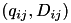 for the joint value
for the joint value 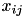 is added. This requires
is added. This requires 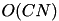 operations.
operations. - We test which other entries
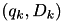 need to be updated. Recall that
need to be updated. Recall that 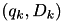 means that, before the merge, the value closest to
means that, before the merge, the value closest to 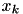 was
was 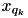 at a distance
at a distance 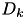 . Then
. Then- If
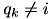 ,
, 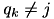 and
and 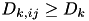 , then
, then 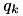 is still the closest element and we do not do anything.
is still the closest element and we do not do anything. - If
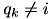 ,
, 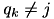 and
and 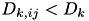 , then the closest element is
, then the closest element is 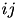 and we update the entry in constant time.
and we update the entry in constant time. - If
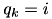 or
or 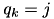 , then we need to re-compute the closest element in
, then we need to re-compute the closest element in 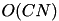 operations.
operations.
- If
This algorithm requires only 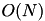 space and
space and 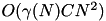 time, where
time, where 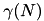 is the expected number of times we fall in the last case. In common cases one has
is the expected number of times we fall in the last case. In common cases one has 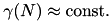 , so the time saving is significant.
, so the time saving is significant.