|
My research lies at the interface of mathematics and
real-world physical phenomena.
I model physical systems using ordinary and partial differential equations
and employ functional analysis,
asymptotic and perturbation analysis, numerical and optimization methods, and most recently data science
to analyze the models in detail.
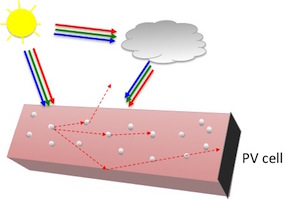
Specifically, my areas of interest include linear and nonlinear wave propagation
and renewable solar energy.
The over-arching goal of my research is to connect between
the mathematical and physical aspects arising from these
problems and make reliable and useful predictions about physical systems.
Below are a few examples from my research
Luminescent solar concentrator
|
