
CURRENT RESEARCH PROJECTS
Imaging with waves
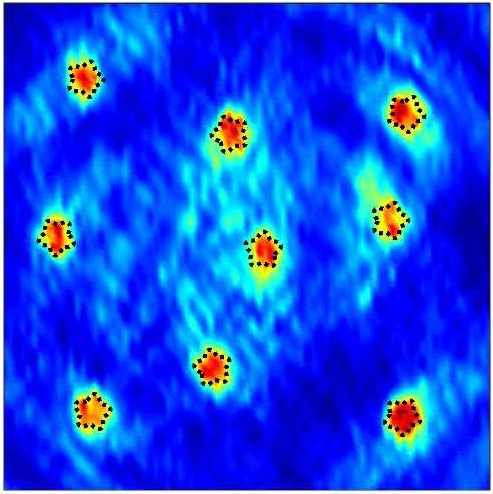
Chrysoula Tsogka and I are studying a broad variety of direct and inverse scattering problems associated with imaging with waves. We have developed several methods for solving inverse scattering problems that have direct application to synthetic aperture radar, space surveillance, buried landmine detection, microscopy and holography, biomedical optical imaging and spectroscopy in tissues, and many others.

Acoustic and optical binding
Dustin Kleckner and I are developing computational models for multiple scattering of acoustic and electromagnetic waves by colloids and their resulting radiation forces. These fundamental models are needed to understand the potential for self-assembly useful in creating new structures on demand.
RECENT PAST RESEARCH PROJECTS
Asymptotic analysis of radiative transfer
Boaz Ilan and I have applied asymptotic analysis to various elementary problems in radiative transfer. Our focus was on developing asymptotic theories that enabled the interpretion of non-invasive measurements of light backscattered by a multiple scattering medium. Our results provide insight into the information on the optical properties of a multiple scattering medium contained in backscattered light.

Modeling 3D nano-assembled plasmonic meta structures
Sayantani Ghosh, Md. Imran Khan and I developed multiscale modeling and simulation of plasmonic meta structures composed of a spherical core surrounded by a shell of metal nanoparticles. We have introduced a new fully three-dimensional model for this system that explicitly incorporates multiple scattering by the core and the metal nanoparticles. This new model can account for system sizes that are larger than previous models were able to consider which is important for practically realizable systems.
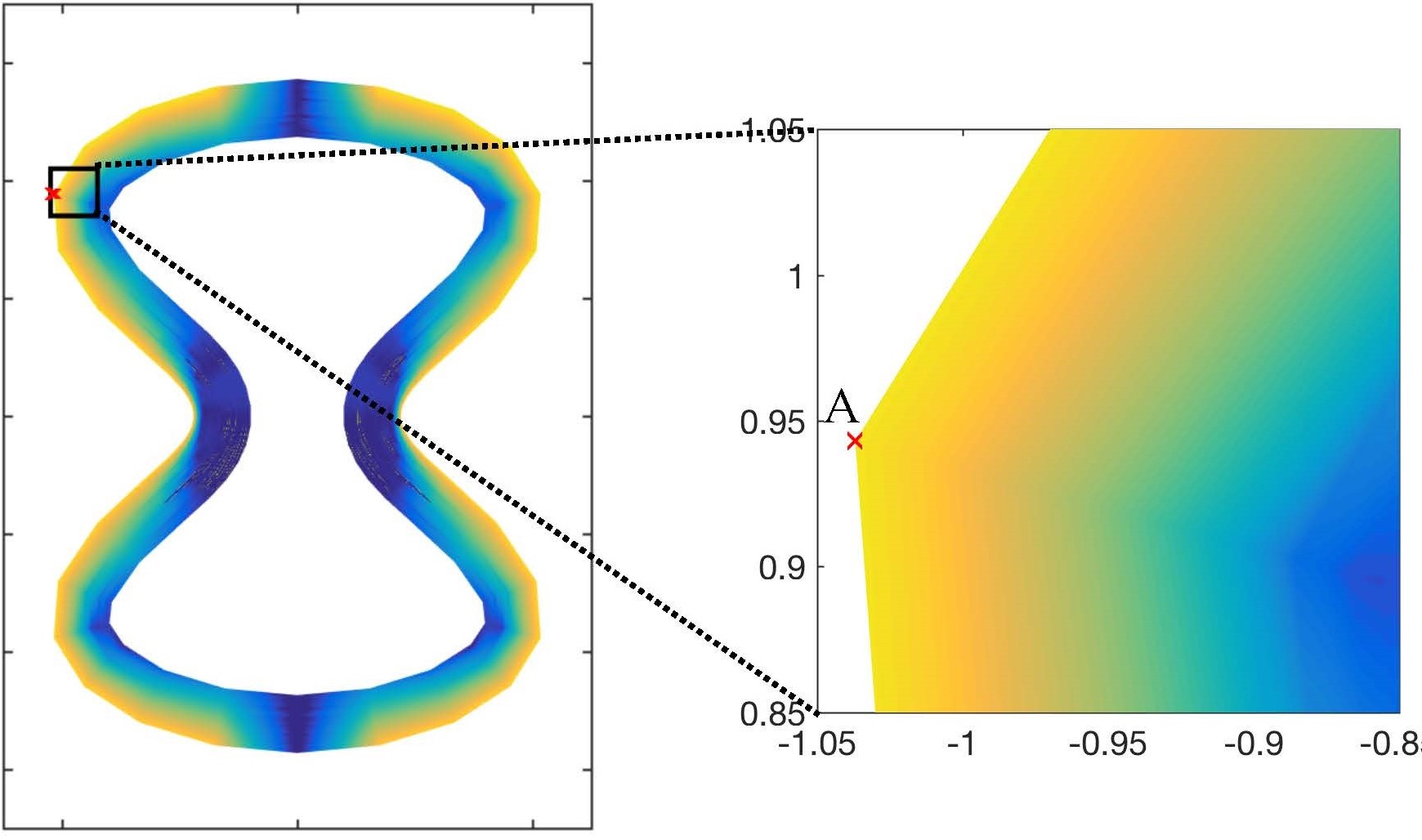
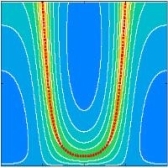
Boundary integral equations
Camille Carvalho, Shilpa Khatri and I developed methods to address fundamental technical challenges with using boundary integral equation methods to solve boundary value problems. At this point we have developed an extensive asymptotic theory that we are now applying to physical problems in electromagnetics and fluid mechanics. Cory McCullough is working with Camille Carvalho and me on boundary integral equation methods to study the coupling between near- and far-field scattering of waves by multiple objects.
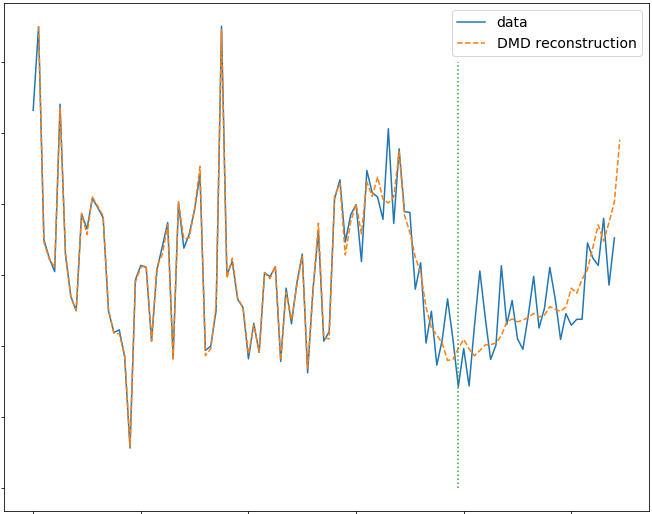
Data science for social justice
Maia Powell, and I investigated problems at the interface between data science and social justice. This research has led me to develop two different collaborations. One collaboration was with Suzanne Sindi and her group studying natural language processing. We developed methods that seek to analyze underlying mathematical structures of hate-speech. The other collaboration was with Paul Smaldino on studying covert signaling in the context of racism in social media.

Data science for gamification
Jeffrey Yoshimi, Tim Meyer, and I applied data science methods for gamification. In particular, we studied complex mouse-tracking time series data from games and developing quantitative techniques and methods to extract useful information from them such as accuracy, gaming experience, and possibly engagement.